1. Block matching method
OpenCV function : cvCalcOpticlFlowBM
원리 : Block matching 방식은 프레임을 일정한 크기의 블록으로 나누고 현재 블록과 가장 유사한 블록을 이전 프레임에서 찾아 그 블록으로 현재의 블록을 추정하는 방법
단점 : Block Matcing 방법의 움직임 벡터 추정 과정에서 가장 정확한 값을 알아내기 위해서는 블록 주변의 모든 변위에 대해 평균 절대값 차이를 계산해야 한느데, 이 때 윈도우 크기가 커질수록 많은 연산 시간을 요구한다. 또한 블록 크기에 따라 벡터의 크기가 한정적이 되므로 움직임 벡터를 찾는데 있어서 제약이 따른다.
장점 : 블록 움직임 추정 방법 중 탐색 영역 내에 후보 블록 과의 차이를 비교하여 유사한 블록을 찾기 때문에 예측 효율과 정확도가 뛰어나다.
- C:
cvCalcOpticalFlowBM(const CvArr* prev, const CvArr* curr, CvSize block_size, CvSize shift_size, CvSize max_range, int use_previous, CvArr* velx, CvArr* vely)
- Python:
cv.CalcOpticalFlowBM(prev, curr, blockSize, shiftSize, max_range, usePrevious, velx, vely) → None Parameters: - prev – First image, 8-bit, single-channel
- curr – Second image, 8-bit, single-channel
- block_size – Size of basic blocks that are compared
- shift_size – Block coordinate increments
- max_range – Size of the scanned neighborhood in pixels around the block
- use_previous – Flag that specifies whether to use the input velocity as initial approximations or not.
- velx –
Horizontal component of the optical flow of
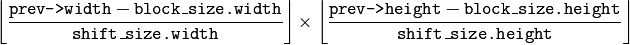
size, 32-bit floating-point, single-channel
- vely – Vertical component of the optical flow of the same size
velx, 32-bit floating-point, single-channel
2. Horn-Schunck algorithm
OpenCV function : cvCalcOpticalFlowHS
원리 : Horn-Schunck algorithm은 발기 향상성 가정을 이용하여 발기 향상성 수식을 계산한 방법이며, 속도 vx, vy의 smoothness constraint를 가정하여 해를 계산한다.
단점 : 대표적인 dense optical flow로써 영상 내부의 모든 픽셀의 속도를 계산하므로 느리다는 단점이 있다.
장점 : 영상 모든 픽셀을 탐색하는 알고리즘으로써 다른 알고리즘보다 정확하다는 장점이 있다.
C: void cvCalcOpticalFlowHS(const CvArr* prev, const CvArr* curr, int use_previous, CvArr* velx, CvArr* vely, double lambda, CvTermCriteria criteria)
- Python:
cv.CalcOpticalFlowHS(prev, curr, usePrevious, velx, vely, lambda, criteria) → None Parameters: - prev – First image, 8-bit, single-channel
- curr – Second image, 8-bit, single-channel
- use_previous – Flag that specifies whether to use the input velocity as initial approximations or not.
- velx – Horizontal component of the optical flow of the same size as input images, 32-bit floating-point, single-channel
- vely – Vertical component of the optical flow of the same size as input images, 32-bit floating-point, single-channel
- lambda – Smoothness weight. The larger it is, the smoother optical flow map you get.
- criteria – Criteria of termination of velocity computing
The function computes the flow for every pixel of the first input image using the Horn and Schunck algorithm [Horn81]. The function is obsolete. To track sparse features, use calcOpticalFlowPyrLK(). To track all the pixels, use calcOpticalFlowFarneback().
3. Lucas-Kanade algorithm
OpenCV function : cvCalcOpticalFlow
원리 : 한 프레임의 각 픽셀 윈도우를 설정하고 다음 프레임에서 이 윈도우와 가장 잘 매칭되는 곳을 찾는다.
단점 : 좁은 지역의 윈도우를 사용하기 때문에 이 윈도우보다 큰 움직임이 발생하였을 경우 움직임을 계산하지 못한다는 단점이 있고, 특징점을 사용하여 Optical Flow를 얻기 때문에 Dense Optical flow에 비해서 정확도가 낮은 편이다.
장점 : Lucas-Kanade algorithm은 Sparse optical flow에 속하여 코너와 같이 두드러지는 특징점을 사용하여 Optical Flow를 추적하기 때문에 연산량이 적다는 장점이 있다.
4. Iteratice Lucas-Kanade method with pyramids
OpenCV function : calcOpticalFlowPyrLK
원리 : Lucas-Kanade 방법에서 큰 움직임을 계산하지 못하는 단점을 개선하기 위해 고안되어진 방법으로 원본 영상으로부터 영상 스케일에 따른 영상 피라미드를 구성한다.
단점 : 몇 개의 특징 점을 추출하고 그 특징점에 대하여 Optical Flow를 계산하기 때문에 Dense optical flow 보다는 정확성이 떨어진다는 단점이 있다.
장점 : 영상 피라미드의 상위계층에서 하위계층으로 추적하면서 다양한 스케일의 이미지를 탐색하기 때문에 커다란 움직임도 찾아 낼 수 있다.
- C++:
calcOpticalFlowPyrLK(InputArray prevImg, InputArray nextImg, InputArray prevPts, InputOutputArray nextPts, OutputArray status, OutputArray err, Size winSize=Size(21,21), int maxLevel=3, TermCriteria criteria=TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 0.01), int flags=0, double minEigThreshold=1e-4 )
- Python:
cv2.calcOpticalFlowPyrLK(prevImg, nextImg, prevPts[, nextPts[, status[, err[, winSize[, maxLevel[, criteria[, flags[, minEigThreshold]]]]]]]]) → nextPts, status, err
- C:
cvCalcOpticalFlowPyrLK(const CvArr* prev, const CvArr* curr, CvArr* prev_pyr, CvArr* curr_pyr, const CvPoint2D32f* prev_features, CvPoint2D32f* curr_features, int count, CvSize win_size, int level, char* status, float* track_error, CvTermCriteria criteria, int flags)
Python: cv.CalcOpticalFlowPyrLK(prev, curr, prevPyr, currPyr, prevFeatures, winSize, level, criteria, flags, guesses=None) -> (currFeatures, status, track_error)
| Parameters: |
|
|---|
5. Build optical Flow Pyramid
OpenCV function : calcOpticalFlowPyrLK
- C++:
buildOpticalFlowPyramid(InputArray img, OutputArrayOfArrays pyramid, Size winSize, int maxLevel, bool withDerivatives=true, int pyrBorder=BORDER_REFLECT_101, int derivBorder=BORDER_CONSTANT, bool tryReuseInputImage=true)¶
- Python:
cv2.buildOpticalFlowPyramid(img, winSize, maxLevel[, pyramid[, withDerivatives[, pyrBorder[, derivBorder[, tryReuseInputImage]]]]]) → retval, pyramid Parameters: - img – 8-bit input image.
- pyramid – output pyramid.
- winSize – window size of optical flow algorithm. Must be not less than
winSizeargument ofcalcOpticalFlowPyrLK(). It is needed to calculate required padding for pyramid levels. - maxLevel – 0-based maximal pyramid level number.
- withDerivatives – set to precompute gradients for the every pyramid level. If pyramid is constructed without the gradients then
calcOpticalFlowPyrLK()will calculate them internally. - pyrBorder – the border mode for pyramid layers.
- derivBorder – the border mode for gradients.
- tryReuseInputImage – put ROI of input image into the pyramid if possible. You can pass
falseto force data copying.
Returns: number of levels in constructed pyramid. Can be less than
maxLevel.
6. Gunnar Farneback's algorithm
OpenCV function : calcOpticalFlowFarneback
원리 : 이 알고리즘은 인접한 두 프레임 간의 움직임을 확장 다항식 기반으로 계산하는 dense optical flow의 한 종류이다.
단점 : dense optical flow 특성상 계산과정이 복잡하여 계산시간이 오래걸린다.
장점 : dense optical flow algorithm은 모든 픽셀들의 값에 대한 optical flow를 계산하므로 정확도가 높다. 특히 이 알고리즘은 평균 에러가 2.00 degree로 Lucas-Kanade 알고리즘 보다도 낮은 평균 에러를 갖는다.
- C++:
calcOpticalFlowFarneback(InputArray prev, InputArray next, InputOutputArray flow, double pyr_scale, int levels, int winsize, int iterations, int poly_n, double poly_sigma, int flags)
- C:
cvCalcOpticalFlowFarneback(const CvArr* prev, const CvArr* next, CvArr* flow, double pyr_scale, int levels, int winsize, int iterations, int poly_n, double poly_sigma, int flags)
- Python:
cv2.calcOpticalFlowFarneback(prev, next, pyr_scale, levels, winsize, iterations, poly_n, poly_sigma, flags[, flow]) → flow Parameters: - prev – first 8-bit single-channel input image.
- next – second input image of the same size and the same type as
prev. - flow – computed flow image that has the same size as
prevand typeCV_32FC2. - pyr_scale – parameter, specifying the image scale (<1) to build pyramids for each image;
pyr_scale=0.5means a classical pyramid, where each next layer is twice smaller than the previous one. - levels – number of pyramid layers including the initial image;
levels=1means that no extra layers are created and only the original images are used. - winsize – averaging window size; larger values increase the algorithm robustness to image noise and give more chances for fast motion detection, but yield more blurred motion field.
- iterations – number of iterations the algorithm does at each pyramid level.
- poly_n – size of the pixel neighborhood used to find polynomial expansion in each pixel; larger values mean that the image will be approximated with smoother surfaces, yielding more robust algorithm and more blurred motion field, typically
poly_n=5 or 7. - poly_sigma – standard deviation of the Gaussian that is used to smooth derivatives used as a basis for the polynomial expansion; for
poly_n=5, you can setpoly_sigma=1.1, forpoly_n=7, a good value would bepoly_sigma=1.5. - flags –
operation flags that can be a combination of the following:
- OPTFLOW_USE_INITIAL_FLOW uses the input
flowas an initial flow approximation. - OPTFLOW_FARNEBACK_GAUSSIAN uses the Gaussian
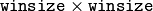 filter instead of a box filter of the same size for optical flow estimation; usually, this option gives z more accurate flow than with a box filter, at the cost of lower speed; normally,
filter instead of a box filter of the same size for optical flow estimation; usually, this option gives z more accurate flow than with a box filter, at the cost of lower speed; normally, winsizefor a Gaussian window should be set to a larger value to achieve the same level of robustness.
- OPTFLOW_USE_INITIAL_FLOW uses the input
(그림 1) PyramidLK, Lucas_kanade, Farneback 소요시간 비교
calcOpticalFlowPyrLK 방식 수행 결과
calcOpticalFlowFarneback 방식 수행 결과
실시간 환경에 적용하기 위해서는 calcOpticalFlowPyrLK 방법이 소요시간이 가장 적고 정확성 또한 괜찮은 결과를 가져다 주므로 이 방법을 선택하는 것이 옳다고 볼 수 있다. 반면 Farneback optical flow의 경우 dense optical flow algorithm 방식으로 수행하기 때문에 정확도는 높지만 알고리즘 소요시간이 상당히 걸리므로 실시간 환경에 적용하기에는 알맞지 않은 방식이라고 볼 수 있다. 계산량이 점차 많아져 윈도우 사이즈가 크거나 실시간 환경에 적용해야 하는 경우에는 수행시간이 빠르고, 계산량이 어느정도 간단하며, 정확도도 어느정도 갖추고 있는 알고리즘을 사용해야 한다. 하지만, 정확한 판단을 요하는 문제에 적용 할 경우 Farneback optical flow를 적용하는 것이 알맞다.
참고자료 1 : http://m.blog.naver.com/hms4913/220126252051
참고자료 2 : http://funvision.blogspot.kr/2016/02/opencv-31-tutorial-optical-flow.html
'AI Research Topic > Object Tracking' 카테고리의 다른 글
| [Object Tracking] Two-Step MOT vs One-Shot MOT (0) | 2020.06.22 |
|---|---|
| [Object Tracking] SiamMask (0) | 2019.12.27 |
| [Object Tracking] SVM을 이용한 HOG 기반 객체 추적 (0) | 2017.02.01 |
| [Object Tracking] 객체 탐지 및 추적 방법 (2) (3) | 2016.10.08 |
| [Object Tracking] 객체 탐지 및 추적 방법 (1) (2) | 2016.09.24 |
꾸준희님의
글이 좋았다면 응원을 보내주세요!



