[Deep Learning] 회귀분석 (Regression) 과 경사하강법 (Gradient Descent)
참고자료 1 : medium.com/mathpresso
참고자료 2 : http://gdyoon.tistory.com/9
참고자료 3 : 텐서플로 첫걸음 (한빛미디어)
1. 회귀분석 (Regression)
Pose Estimation에 대한 자료를 찾다보면 Keypoints detection에서 heatmap을 이용한 포즈추정시 Regression 이라는 개념이 많이 등장한다. 사실 이 개념은 머신러닝에서 나오는 개념이며, 이번 기회에 정리해보도록 한다.
회귀분석이란 주어진 데이터가 어떤 함수로부터 생성되었는가를 알아보는 '함수 관계'를 추측하는 것이다. 즉, 훈련 데이터세트 (X, Y) 로 부터 학습알고리즘을 이용하여 가설을 생성하고, 생성된 가설에 데이터를 입력하여 예측 값 데이터를 얻는 것이다. 이러한 가설에 해당하는 식이 어떤 방정식인지, 계수는 어떤 것을 의미하는지 알아가는 과정이라고 할 수 있다.
방정식의 계수가 선형인 경우 선형 회귀 분석 (Linear Regression Analysis) 라고 하고, 방정식의 계수가 여러개이면 다중 선형 회귀 분석 (Multiple Linear Regression Analysis) 라고 한다.
앞서 텐서플로우를 이용한 선형회귀분석 포스팅에서 다루었던 테스트 데이터와 아래 데이터를 가장 잘 표현 할 수 있는 함수를 찾은 결과이다.

테스트 데이터는 y=x 그래프에 약간의 오차를 섞어 만든 데이터이고, 학습을 통해 데이터에 맞는 가중치 값 w와 편향 값 b를 찾아 수행한 결과이다.
y = w * x + b
의 식을 정의하여 결과 값과의 오차를 Gradient Descent를 사용하여 학습하여 알맞는 함수를 찾을 수 있다.
데이터에 대한 가설을 학습할 때 그려진 선과 각 데이터의 분포의 차이를 계산하여 차이가 가장 적은 것이 이 모델에 적합한 선이라는 것을 알 수 있다. 이를 비용함수(Cost Function) 이라고 한다. 이 비용함수를 이용하여 실제 세운 가설과 나타내는 값이 얼마나 다른지를 생각해볼 수 있다.
즉, 비용함수(오차함수)는 두 개의 매개변수(w, b) 로 구성되어 있으므로 이를 2차원 공간에 표현 할 수 있다. 각 점에서 오차함수의 높이는 직선에 대한 오차이며, 어떤 직선들은 다른 직선들보다 더 작은 오차를 가지게 된다. 가령 텐서플로우에서 경사 하강법 알고리즘을 수행할 때 이 평면의 한 지점에서 시작하여 더 작은 오차를 갖는 직선을 찾아 이동해나간다.
또한, 오차함수의 기울기를 계산하기 위하여 오차함수를 미분하는 과정을 거치게 된다. 직선을 찾아가는 과정의 반복이 있을 때 마다 움직일 방향을 알아가기 위해 W와 b에 대한 편미분 방정식 계산이 필요하다.
다중 회귀 분석은 단일 회귀 분석에서 쓰였던 입력데이터 x가 2개 이상이 된다. 두개의 변수(x1, x2)를 갖는 다중 회귀 분석의 경우 아래와 같이 정의하고 학습하여 데이터에 맞는 평면을 찾을 수 있다.
y = w1 * x1 + w2 * x2 + b
이러한 단일, 다중 회귀 분석을 통하여
"어느 데이터가 존재하면 그 데이터를 표현하는 함수를 학습 할 수 있다는 것"을 알 수 있다.
2. 경사하강법 (Gradient Descent)
경사하강법 이란 cost 비용을 최소화 하기 위한 최적화 알고리즘이다. 최적화란 여러 가지 허용되는 값들 중에서 주어진 기준을 가장 잘 만족하는 것을 선택하는 것이다. 해당 함수의 최솟값 위치를 찾기 위해 비용함수의 기울기 반대 방향으로 정의한 Step Size를 가지고 조금씩 움직이면서 최적의 파라미터를 찾는 과정이라고 할 수 있다.
즉, 경사하강법은 기울기로 함수의 최솟값을 찾는 방법이다. 특히나 신경망에서 오류역전파(Backpropagation)를 수행 할 때 오류의 최솟값을 찾는데 사용된다.
여기서 기울기(Gradient)는 파라미터에 대해 편미분한 벡터를 의미하며, 이 파라미터를 반복적으로 조금씩 움직이는 것이 관건이다. 이 때 머신러닝에서는 가장 간단한 모델인 선형 회귀(Linear Regression)이 대표적이다.
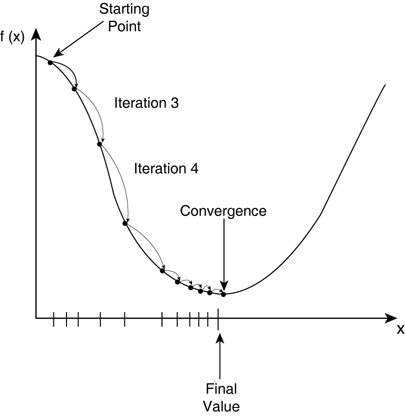
다음 그림과 같이, 가장 낮은 곳에 위치하는 x 값을 찾아가는 과정이다.
이 x 값을 찾아가기 위해 접선의 기울기인 함수의 미분을 사용하여 찾게 된다. 자세한 식은 (참조)
함수 최적화 방법인 경사하강법 알고리즘은 Greedy 방식을 사용한다. 이것은 휴리스틱(Heuristic) 한 탐색을 하기 때문에 Local Minimum 을 가질 위험이 있다. 이때 해결하기 위한 매커니즘으로는 Convex Function 등이 있다.
'AI Research Topic > Deep Learning' 카테고리의 다른 글
| [Deep Learning] CNN(Convolutional Neural Network) (1) | 2018.11.01 |
|---|---|
| [Deep Learning] 손글씨 인식 (MNIST) (1) | 2017.08.25 |
| [Deep Learning] pre-training 과 fine-tuning (파인튜닝) (0) | 2017.08.17 |
| [Deep Learning] end-to-end trainable neural network (3) | 2017.08.04 |
| [Deep Learning] 7. 2층 신경망 구현하기 (0) | 2017.07.17 |