[선형대수학 및 기타 수학] 최대 우도 추정 (Maximum Likelihood Estimation)
최대 우도 추정 (aximum Likelihood Estimation)
최대 우도 추정 (aximum Likelihood Estimation) 은 모수 (parameter)가 미지의 θ 인 확률분포에서 뽑은 표본 x 들을 바탕으로 θ를 추정하는 기법이다. 여기서 우도(likelihood)란 이미 주어진 표본 x 들에 비추어 봤을 때 모집단의 모수 θ 에 대한 추정이 그럴듯한 정도를 말한다. 우도 L( θ | x ) 는 θ 가 전제되었을 때 표본 x 가 등장할 확률인 p( x | θ ) 에 비례한다.
동전 던지기 100번을 수행하는 예시에서 반복적인 동전던지기는 성공 확률이 p 인 베르누이 시행을 n 번 반복 시행할 때 성공 횟수의 분포인 이항분포(binomial distribution)를 따른다. 이 예시에서 미지의 모수 θ 는 동전을 한 번 던졌을 때 앞면이 나올 확률 p 가 된다. 이를 위해 앞면이 나올 확률이 p 인 이항분포에서 뽑은 표본 x 를 활용한다.
이항분포의 확률 함수는 다음과 같다.
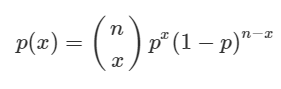
이 동전이 앞면 뒷면 나올 확률이 (θ =0.5) 라고 가정하고 우도를 계산하면 다음과 같다.

이와 같은 방법으로 θ 값을 변형해가며 우도를 계산하면 다음과 같다.
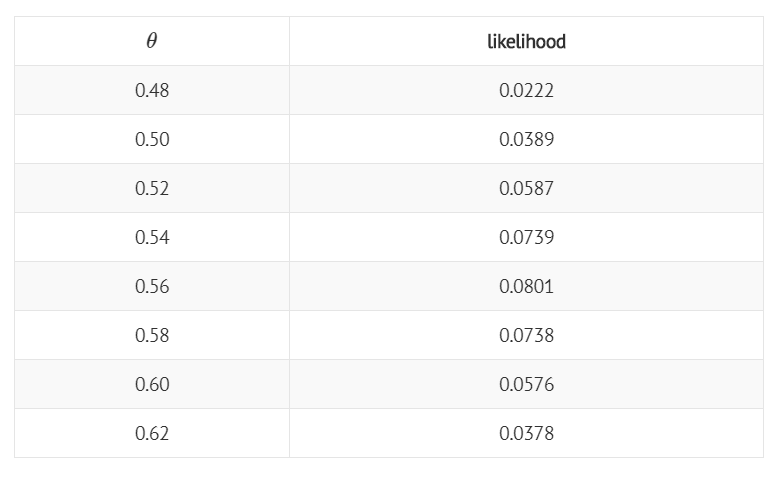
그래프로 그려보면 다음과 같다.

이 이항분포의 확률함수와 그래프를 보면 미분이 가능하다.
따라서 θ 에 대해 편미분을 해 0이 되는 지점을 구하면 우도를 최대화 하는 θ 를 구할 수 있다.
하지만 미분이 불가능할 경우에는 그래디언트 디센트 등 반복적이고 점진적인 방식으로 θ 를 추정하게 된다. 로지스틱 회귀나 딥러닝 등 모델의 θ 를 최대 우도 추정 기법으로 추정할 때 자주 쓰이는 기법이다.
참고자료 1 : https://ratsgo.github.io/statistics/2017/09/23/MLE/
최대우도추정(Maximum Likelihood Estimation) · ratsgo's blog
이번 글에서는 최대우도추정(Maximum Likelihood Estimation)에 대해 살펴보도록 하겠습니다. 이 글은 Ian Goodfellow 등이 집필한 Deep Learning Book과 위키피디아, 그리고 조현제 님의 자료를 정리했음을 먼저 �
ratsgo.github.io
참고자료 2 : http://jaejunyoo.blogspot.com/2018/02/minimizing-negative-log-likelihood-in-kor.html
Minimizing the Negative Log-Likelihood, in Korean (1)
Machine learning and research topics explained in beginner graduate's terms. 초짜 대학원생의 쉽게 풀어 설명하는 머신러닝
jaejunyoo.blogspot.com
'Computer Science > 선형대수학 및 기타 수학' 카테고리의 다른 글
| 수학 기호 정리 (6) | 2022.08.13 |
|---|---|
| [선형대수학] 딥러닝에서의 노름 혹은 놈(Norm) (0) | 2020.12.10 |
| P문제와 NP문제(NP-hard) (0) | 2019.02.17 |
| 수학기호 정리 (2) | 2018.02.23 |
| [선형대수학] PCA & PPCA (0) | 2018.02.06 |